Modelos Matemáticos: La curva de Malthus

[Anselmo]

 Como aperitivo de una serie de escarceos con el tema de modelos matemáticos, dirigido a los lectores de este foro que están  poco o nada duchos en estas lides, vamos a comenzar tratando con el modelo de crecimiento de población enunciado por Malthus, modelo que ha servido de justificación  a una serie de creencias que han tenido y tienen  una gran influencia en no pocos acontecimientos históricos  .    Solicito la indulgencia de quienes sean conocedores de estos temas, dado que la finalidad de  este post es meramente divulgativa.

                                          *********************

Malthus en 1798 escribió que, cuando no lo impide ningún obstáculo,  la población se duplica cada veinticinco años. Para ello se basó en los datos del censo de población de los Estados Unidos.

Vamos a partir del dato de que la población en Estados Unidos en 1700 era de 250 888, y que si se duplica cada 25 años  vienea aswer casi lo mismo que afirmar que cada año crece un 3%.

Población inicial 250 888, que cada año  crece un 3%:

La población al final de cada año será igual a la población al final del año anterior multiplicada por
 (1 +3%) ,o lo que es lo mismo por 1,03 .  Así la población a finales del primer año será de 250 888 multiplicado por  1,03 =258414

. La población del segundo año será 258414 multiplicado por 1,0 3  =266167

, y así sucesivamente.

Si empleamos una hoja Excel

Ponemos en la casilla F5 lo siguiente    =250888

Ponemos en la casilla F6 lo siguiente =F5*1,0 3  pulsamos “enter”

Situamos el ratón en la casilla F6, pulsamos el botón derecho y seleccionamos copiar

Situamos el ratón en la casilla F7 pulsamos con el botón izquierdo y manteniéndolo pulsado lo movemos hacia abajo por la misma columna,   hasta la celda, por ejemplo, 150, creando una zona tintada de color azul .Dejamos de pulsar el botón izquierdo, situamos el ratón sobre cualquier punto de la zona azulada ( o grisácea) , pulsamos el botón derecho y ,en opciones de pegado, elegimos la primera opción, con lo que se habrá calculado la población para muchos años consecutivos. De acuerdo con los números obtenidos vemos que el contenido de la celda F105, correspondiente a la población de los Estados Unidos en el  año 1800, supera los 46 millones.

Si queremos representarlo gráficamente.

Seleccionamos con el ratón la casilla F5, sin levantar el dedo del ratón lo desplazamos columna abajo mientras hayan celdas con números. En la parte superior de la pantalla clicamos con el botón izquierdo del ratón sobre “insertar” y después seleccionamos en gráficos “dispersión”. Elegimos cualquiera de las opciones de gráficos que se nos presenta , y obtenemos la representación gráfica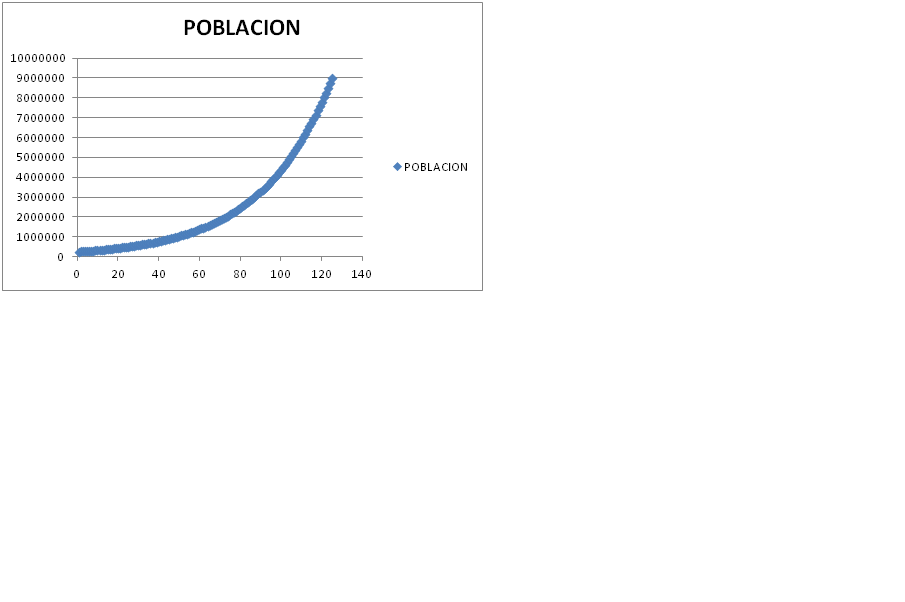


 
Si se comparan los datos obtenidos basándonos en lo dicho por Malthus y los datos disponibles sobre la población  estadounidense durante el siglo 18, veremos que concuerdan muy bien.
 

 Pero no debemos olvidar que Malthus no tuvo en cuenta la contribución de la inmigración.

[Crosscountry]

pues dicho así parece que al final tendremos un problema...

los modelos matemáticos son validos para explicar la realidad y sirven de base para afrontar los problemas pero cuidado con ellos, la realidad es un poco mas compleja y mas cuando se trata de seres humanos.

si a los modelos les añadimos algoritmos genéticos para que puedan evolucionar entonces tendremos un modelo que se acerque mas a realidad que con reglas fijas.

aunque reglas sencillas siempre pueden sorprendernos con el extraño pero real " comportamiento emergente ".

http://www.ucasal.edu.ar/htm/ingenieria/cuadernos/archivos/3-p46-Venturini.pdf

Anselmo muy bien por abrir el hilo... este tema tiene mas miga de lo que parece...

[Anselmo]

He detectado un error que os ruego me disculpéis.

Me he dado cuenta de que el valor que propuse para la constante de crecimiento de la población, nuestra “K”, no es del 4% anual sino del 2,9% anual. Es decir en la hoja Excel tendríamos que introducir el cambio de F6=F5*1,029 y volver a realizar los pasos correspondientes.

Obtendríamos una población para el año 1800 de cuatro millones trescientos setenta y cinco mil  habitantes, que  si concordarían bastante con los del censo (1), tal como se ve en el siguiente gráfico.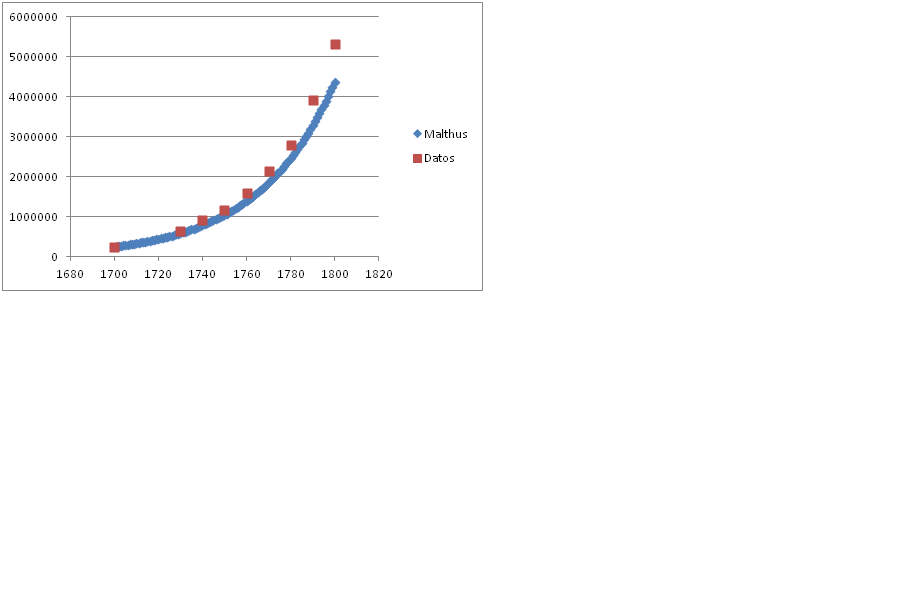




 


¿En qué medida los  datos de Malthus sobre crecimiento de la población de los Estados Unidos podrían haberse extrapolado hasta el presente?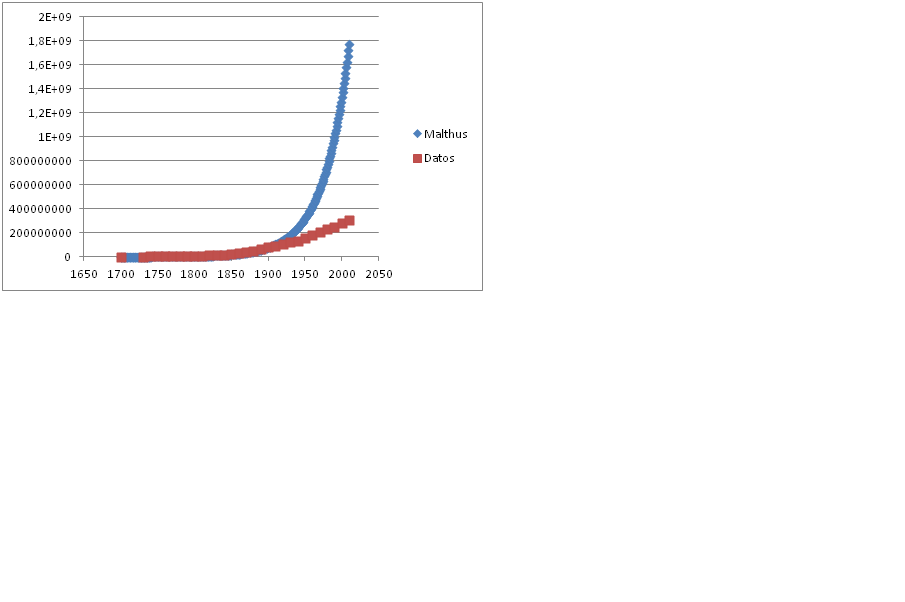




 

La respuesta es que en ninguna

Nota

(1) https://en.wikipedia.org/wiki/Demographic_history_of_the_United_States

[Crosscountry]

Por eso digo que con seres humanos no es tan fácil aplicar modelos matemáticos... pero si lo es con los mercados de valores podemos discutir sobre eso...

[Anselmo]

LA FUNCIÓN LOGÍSTICA DE VELHURST


En el post sobre Malthus hemos visto que, el modelo que él proponía , describía una duplicación de la  población cada veinticinco años, con lo que esta tendía incrementarse al infinito. Lo que significaba que periódicamentese sufrirían hambrunas.

La experiencia indica que, aunque crecimientos de tipo maltusiano se dan  en determinadas poblaciones biológicas, lo  normal es que las poblaciones de mamíferos  tiendan a crecer al principio exponencialmente, pero que ese crecimiento se vaya suavizando hasta alcanzar cierto nivel en el que el tamaño de las poblaciones deja de incrementarse.

Esto lo expresó un tal Velhurst  con una ecuación, cuya expresión en diferencias es

N (t+1)    =N(t)*r*(M-N(t))/M + N(t)
Donde

N(t):población a final de año t
N(t+1):población a fin del año siguiente
M: tamaño máximo de la población


En la hoja Excel de Malthus introduciremos los siguientes cambios:

En la celda  B1, introduciremos el valor de K,    =0, 029
En la celda  B3, introduciremos el valor  M que sugiero sea de cuatrocientos millones de habitantes,   = 400000000
En la celda F6 introduciremos la siguiente expresión

=$B$3*$B$1*(F5/$B$3)*(1-F5/$B$3)+F5


Y obtendremos la siguiente curva: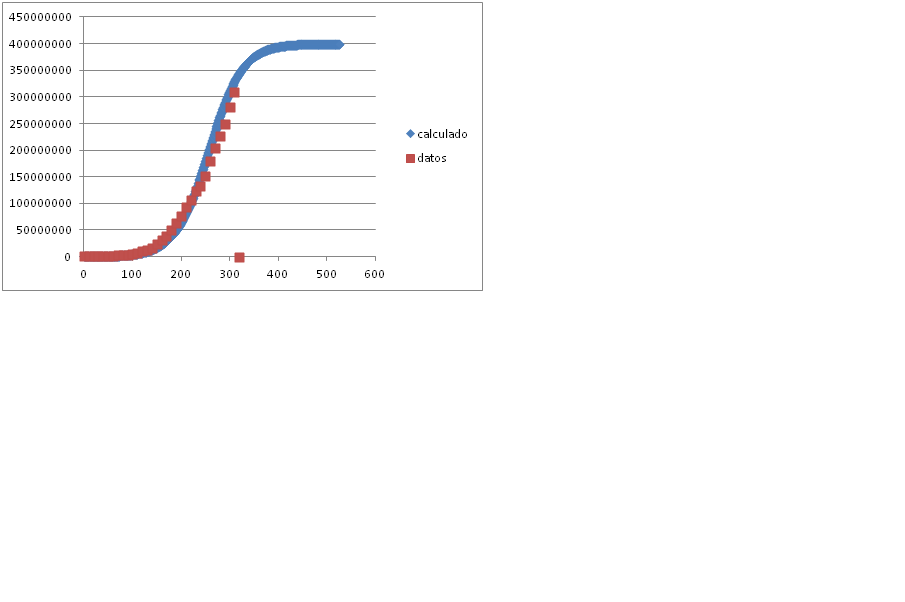


 

Vemos que si suponemos un límite de población de 400 millones, la curva coincide bastante con los datos de que disponemos

[Anselmo]

Obtención de la curva de Hubbert.

Si en la hoja de cálculo,  en la casilla G6 ponemos =$B$3*$B$1*(F5/$B$3)*(1-F5/$B$3) , y lo copiamos para toda la columna(hasta la fila quinientos mas o menos), obtendremos las variaciones de población para cada año,  su representación gráfica será






Nos resultará familiar, en efecto, es muy parecida a la famosa curva de Hubbert.

Si en nuestra hoja de cálculo (para calcular la evolución de la población estadounidense), cambiamos el valor de la constante de crecimiento por el de 0,09, el de la población máxima por 150 000 (millones de barriles), y el de la población inicial por 10 (millones de barriles), las curva que obtendremos serían las de la producción acumulada de petróleo  USA  y la dela producción anual (la curva de variación) a partir de 1860;
El máximo se daría en el año 112 con una producción de 3374 millones de barriles /año,. Dicho de otro modo el máximo se ha alcanzado en el año 1860+ (112-4)=1968, con un valor de 9,24 millones de barriles /día.
Si cambiamos el valor de “r” por 0,07, el de la población máxima por la cifra de 2 millones de millones  de barriles, (pondremos dos millones)   y el de la población inicial por 1200 millones de barriles




El gráfico que obtendremos será bastante aproximado a la curva de  la producción mundial de petróleo, a partir de 1900, con cenit en (1900+110-3)=2007,con un valor de 34999 millones de barriles petróleo .


Las ecuaciones que se han utilizado son algo inexactas, pero favorecen la claridad expositiva. En caso de que algún lector manifieste su interés , estaré encantado de incluir las ecuaciones con el tiempo con valores continuos .

Una vez que tenemos el gráfico de la producción del petróleo, resulta casi inmediato obtener el gráfico de la energía neta obtenida.... Lo veremos en la siguiente entrega.