Re: Modelos Matemáticos: La curva de Malthus
Posted by Anselmo on Ago 23, 2015; 5:16pm
URL: http://foro-crashoil.109.s1.nabble.com/Modelos-Matematicos-La-curva-de-Malthus-tp22348p22598.html
LA FUNCIÓN LOGÍSTICA DE VELHURST
En el post sobre Malthus hemos visto que, el modelo que él proponía , describía una duplicación de la población cada veinticinco años, con lo que esta tendía incrementarse al infinito. Lo que significaba que periódicamentese sufrirían hambrunas.
La experiencia indica que, aunque crecimientos de tipo maltusiano se dan en determinadas poblaciones biológicas, lo normal es que las poblaciones de mamíferos tiendan a crecer al principio exponencialmente, pero que ese crecimiento se vaya suavizando hasta alcanzar cierto nivel en el que el tamaño de las poblaciones deja de incrementarse.
Esto lo expresó un tal Velhurst con una ecuación, cuya expresión en diferencias es
N (t+1) =N(t)*r*(M-N(t))/M + N(t)
Donde
N(t):población a final de año t
N(t+1):población a fin del año siguiente
M: tamaño máximo de la población
En la hoja Excel de Malthus introduciremos los siguientes cambios:
En la celda B1, introduciremos el valor de K, =0, 029
En la celda B3, introduciremos el valor M que sugiero sea de cuatrocientos millones de habitantes, = 400000000
En la celda F6 introduciremos la siguiente expresión
=$B$3*$B$1*(F5/$B$3)*(1-F5/$B$3)+F5
Y obtendremos la siguiente curva:
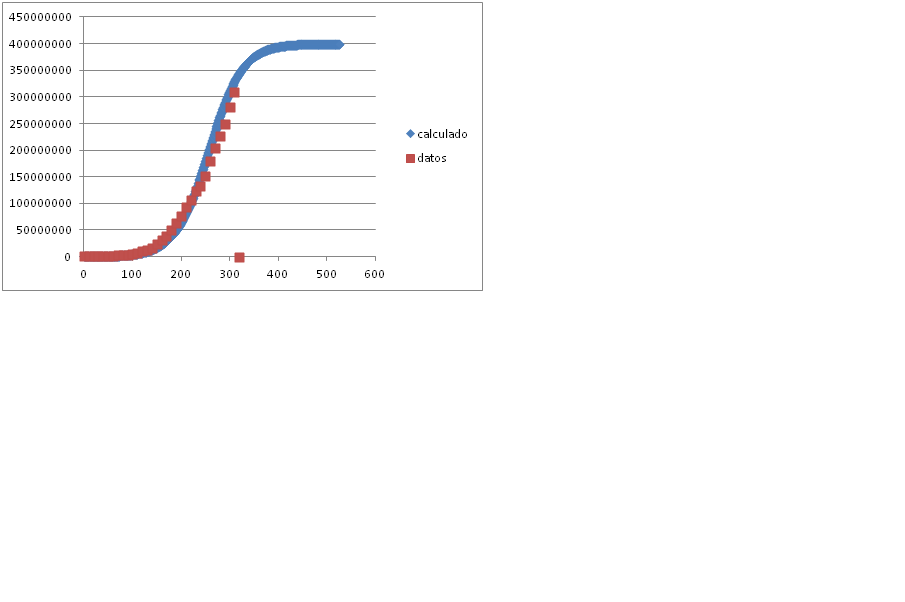
Vemos que si suponemos un límite de población de 400 millones, la curva coincide bastante con los datos de que disponemos
URL: http://foro-crashoil.109.s1.nabble.com/Modelos-Matematicos-La-curva-de-Malthus-tp22348p22598.html
LA FUNCIÓN LOGÍSTICA DE VELHURST
En el post sobre Malthus hemos visto que, el modelo que él proponía , describía una duplicación de la población cada veinticinco años, con lo que esta tendía incrementarse al infinito. Lo que significaba que periódicamentese sufrirían hambrunas.
La experiencia indica que, aunque crecimientos de tipo maltusiano se dan en determinadas poblaciones biológicas, lo normal es que las poblaciones de mamíferos tiendan a crecer al principio exponencialmente, pero que ese crecimiento se vaya suavizando hasta alcanzar cierto nivel en el que el tamaño de las poblaciones deja de incrementarse.
Esto lo expresó un tal Velhurst con una ecuación, cuya expresión en diferencias es
N (t+1) =N(t)*r*(M-N(t))/M + N(t)
Donde
N(t):población a final de año t
N(t+1):población a fin del año siguiente
M: tamaño máximo de la población
En la hoja Excel de Malthus introduciremos los siguientes cambios:
En la celda B1, introduciremos el valor de K, =0, 029
En la celda B3, introduciremos el valor M que sugiero sea de cuatrocientos millones de habitantes, = 400000000
En la celda F6 introduciremos la siguiente expresión
=$B$3*$B$1*(F5/$B$3)*(1-F5/$B$3)+F5
Y obtendremos la siguiente curva:

Vemos que si suponemos un límite de población de 400 millones, la curva coincide bastante con los datos de que disponemos
| Free forum by Nabble | Edit this page |