Re: Introducción a la teoría cuántica de campos (QFT) y la energía del vacío
Posted by Z on Jul 30, 2017; 8:02am
URL: http://foro-crashoil.109.s1.nabble.com/Introduccion-a-la-teoria-cuantica-de-campos-QFT-y-la-energia-del-vacio-tp40610p40649.html
Dario, sobre el tema de la energía oscura. Muchos piensan que la energía oscura está directamente relacionada con la constante cosmológica en las ecuaciones de Einstein de la relatividad general. En concreto dicha constante aparece en el lado derecho de su ecuación fundamental, en la parte de la contribución del tensor de energía-tensión:
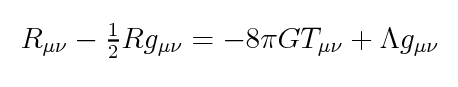
Pero según la relatividad general se supone que este tensor energía-tensión es la suma de TODO lo (energéticamente) existente en cierta región del espacio, por lo que la renormalización y la resta de la "infinita" energía del vacío aquí no aplica. Por lo tanto la constante cosmológica debería poseer un valor de

siendo E0 la (infinita) energía del vacío en cada posición infintesimal del espacio en consideración (V), lo cual evidentemente no cuadra con los datos, puesto que la constante cosmológica se calcula que es una aportación minúscula (finita) en la ecuación de arriba para que los datos cosmológicos (mediante la energía oscura) cuadren.
No sólo eso. Sabemos que el modelo estándar "funciona" hasta niveles de energía de 10^12eV y que predice la existencia de muchos campos cuánticos (uno por cada tipo de partícula), cada uno con su energía de vacío ¡por lo que la suma de la contribución de energía es infinita para cada campo en cada punto infintesimal del espacio!
Es decir, que la constante cosmológica de la ecuación de Einstein (la parte derecha) debería poseer siempre un valor infinito en todo momento, lo cual es absurdo. Es evidente que algo no cuadra para nada en la física moderna. O simplemente la teoría cuántica de campos no es válida, o la relatividad general no es válida, o se trata de que ambas son buenas aproximaciones pero hay un "algo más" que cancela toda esa infinita energía del punto cero para cada campo, dejando como resultado una cantidad residual finita que es la que la constante cosmológica tiene en cuenta.
En fin, que nadie sabe la respuesta y lo peor es que no hay ninguna buena pista de por donde buscar la solución a este problema de la constante cosmológica.
URL: http://foro-crashoil.109.s1.nabble.com/Introduccion-a-la-teoria-cuantica-de-campos-QFT-y-la-energia-del-vacio-tp40610p40649.html
Dario, sobre el tema de la energía oscura. Muchos piensan que la energía oscura está directamente relacionada con la constante cosmológica en las ecuaciones de Einstein de la relatividad general. En concreto dicha constante aparece en el lado derecho de su ecuación fundamental, en la parte de la contribución del tensor de energía-tensión:
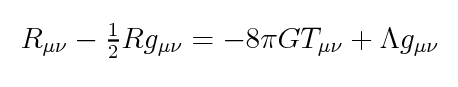
Pero según la relatividad general se supone que este tensor energía-tensión es la suma de TODO lo (energéticamente) existente en cierta región del espacio, por lo que la renormalización y la resta de la "infinita" energía del vacío aquí no aplica. Por lo tanto la constante cosmológica debería poseer un valor de

siendo E0 la (infinita) energía del vacío en cada posición infintesimal del espacio en consideración (V), lo cual evidentemente no cuadra con los datos, puesto que la constante cosmológica se calcula que es una aportación minúscula (finita) en la ecuación de arriba para que los datos cosmológicos (mediante la energía oscura) cuadren.
No sólo eso. Sabemos que el modelo estándar "funciona" hasta niveles de energía de 10^12eV y que predice la existencia de muchos campos cuánticos (uno por cada tipo de partícula), cada uno con su energía de vacío ¡por lo que la suma de la contribución de energía es infinita para cada campo en cada punto infintesimal del espacio!
Es decir, que la constante cosmológica de la ecuación de Einstein (la parte derecha) debería poseer siempre un valor infinito en todo momento, lo cual es absurdo. Es evidente que algo no cuadra para nada en la física moderna. O simplemente la teoría cuántica de campos no es válida, o la relatividad general no es válida, o se trata de que ambas son buenas aproximaciones pero hay un "algo más" que cancela toda esa infinita energía del punto cero para cada campo, dejando como resultado una cantidad residual finita que es la que la constante cosmológica tiene en cuenta.
En fin, que nadie sabe la respuesta y lo peor es que no hay ninguna buena pista de por donde buscar la solución a este problema de la constante cosmológica.
| Free forum by Nabble | Edit this page |